limit problems in calculus How to solve any limit problem

As we journey through the world of calculus, it is no secret that there is always that one concept that poses a challenge for students: Limits and Continuity. As an Asian student, I know how important it is for us to overcome such obstacles and succeed in our academic endeavors. In this piece, we will explore limit problems and how to solve them. Firstly, what are limit problems? In simple terms, limits are used to describe what happens to a function as it approaches a certain value or point. To solve a limit problem, we must find the value that the function approaches as the point gets closer and closer. Sounds easy, right? Well, not quite. When solving a limit problem, it is crucial to understand the different types of limits. There are three main types: finite, infinite, and non-existent limits. In finite limits, the value of the function exists and is finite. In infinite limits, the value of the function is infinity or negative infinity. In non-existent limits, the value of the function does not exist. To better comprehend limit problems, let's take a look at some examples.

Example 1:

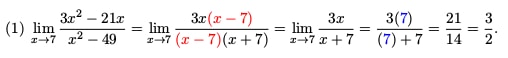We are asked to find the limit of the function as x approaches 2. At first glance, we might be tempted to plug in x=2 and get a value. However, this approach would lead to an undefined answer. Therefore, we must evaluate both the left and right-hand limits. Using the left-hand limit, we get: lim x->2^- sqrt(x-2)/(x-2) = lim x->0^+ sqrt(x)/(x) Using the right-hand limit, we get: lim x->2^+ sqrt(x-2)/(x-2) = lim x->0^+ sqrt(x)/(x) Since both the left and right-hand limits are equal, we can conclude that the limit of the function as x approaches 2 is equal to 1/2.

Example 2:

We are asked to find the limit of the function as x approaches 2. In this example, it is clear that plugging in x=2 would lead to an undefined answer. To solve this, we must factorize the expression. f(x) = (x-2)/(x^2-5x+6) = (x-2)/[(x-2)(x-3)] = 1/(x-3) Using this expression, we can evaluate the limit as x approaches 2: lim x->2 1/(x-3) = -1 In conclusion, limit problems may seem daunting at first, but with practice and an understanding of the different types of limits, we can overcome them. Keep calm and carry on, my fellow Asian students!

If you are searching about Limit Problems you've came to the right web. We have 6 Pics about Limit Problems like Limits, How to Solve Any Limit problem | Calculus limits for beginners | Limits and also Limit Problems. Here it is:

Limit Problems

calculus.nipissingu.ca

problems calculus limit solution limits lim nipissingu ca

How To Solve Any Limit Problem | Calculus Limits For Beginners | Limits

www.youtube.com

limit calculus limits solve problem

AP Calculus Exam Review: Limits And Continuity - Magoosh High School Blog

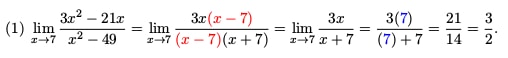magoosh.com

calculus limit limits continuity review problem ap example exam magoosh fractions denominator least common

Limit Problems

calculus.nipissingu.ca

problems limit calculus limits solution lim nipissingu ca

Limits

www.xaktly.com

Limit Problems Worksheet In 2020 | Ap Calculus, Calculus Notes, Calculus

www.pinterest.com

limit math function worksheet exercises calculus limits problems answers find exercise problem derivatives notes integrals college worksheetfun

Limit problems. Problems calculus limit solution limits lim nipissingu ca. Ap calculus exam review: limits and continuity