The following system of differential equations was given:
x'1 = 2x1 - x2
x'2 = 3x1 - 2x2

This system of differential equations can be rewritten in matrix form as Ax' = b, where A = [[2, -1], [3, -2]], x' = [[x'1], [x'2]], and b = [[0], [0]].
To find the general solution of the system, we first need to find the eigenvalues of A. The characteristic equation can be found by taking the determinant of A - λI:
| A - λI | =
| 2 - λ, -1 |
| 3, -2 - λ | =
(2 - λ)(-2 - λ) - (-1)(3) = 0
λ2 - 4λ + 1 = 0
Using the quadratic formula, we get:
λ = 2 ± √3
These are the eigenvalues of A. To find the eigenvectors, we solve the system (A - λI)v = 0 for each eigenvalue.
For λ = 2 + √3, we have:
(0.732v1 - 0.366v2, 0.366v1 - 0.634v2) = (0, 0)
This leads to the eigenvector v = [0.366, 0.634].
Similarly, for λ = 2 - √3, we have:
(-0.732v1 + 0.366v2, -0.366v1 + 0.634v2) = (0, 0)
This leads to the eigenvector v = [0.634, 0.366].
The general solution of the system of differential equations is given by:
x(t) = c1e(2 + √3)t[0.366, 0.634] + c2e(2 - √3)t[0.634, 0.366],
where c1 and c2 are arbitrary constants.
The given system of differential equations is:
x'1 = x1 - x2 + 6e2t
x'2 = 2x1 - x2
We can express this as Ax' = f(t), where
A = [[1, -1], [2, -1]],
x' = [[x'1], [x'2]], and
f(t) = [[6e2t], [0]].
We first need to find the general solution of the homogeneous system Ax' = 0. To do this, we find the eigenvalues and eigenvectors of A.
The characteristic equation is:
| A - λI | =
| 1 - λ, -1 |
| 2, -1 - λ |
(1 - λ)(-1 - λ) + 2 = 0
λ2 - λ - 1 = 0
Using the quadratic formula, we get:
λ = (1 ± √5)/2
These are the eigenvalues of A. To find the eigenvectors, we solve the system (A - λI)v = 0 for each eigenvalue.
For λ = (1 + √5)/2, we have:
(0.618v1 - v2, 2v1 - v2) = (0, 0)
This leads to the eigenvector v = [1, 0.618].
Similarly, for λ = (1 - √5)/2, we have:
(-0.618v1 + v2, -2v1 + v2) = (0, 0)
This leads to the eigenvector v = [1, -0.618].
The general solution of the homogeneous system Ax' = 0 is given by:
xh(t) = c1e(1 + √5)t/2[1, 0.618] + c2e(1 - √5)t/2[1, -0.618],
where c1 and c2 are arbitrary constants.
Now, we need to find a particular solution of the system Ax' = f(t). We can use the method of undetermined coefficients to guess a particular solution of the form xp(t) = ae2t. Substituting this into the system, we get:
a = 3/4
Therefore, the general solution of the system Ax' = f(t) is:
x(t) = xh(t) + xp(t) = c1e(1 + √5)t/2[1, 0.618] + c2e(1 - √5)t/2[1, -0.618] + (3/4)e2t,
where c1 and c2 are arbitrary constants.
If you are looking for Solved: Find The General Solution To The Given System Of D... | Chegg.com you've visit to the right place. We have 6 Images about Solved: Find The General Solution To The Given System Of D... | Chegg.com like Solved Apply the eigenvalue method to find a general | Chegg.com, Solved Find the general solution of the given system. X' = | Chegg.com and also Solved Apply the eigenvalue method to find a general | Chegg.com. Read more:
Solved: Find The General Solution To The Given System Of D... | Chegg.com
 www.chegg.com
www.chegg.com solution general solved given system find transcribed problem text been
Solved: Find The General Solution Of The Given System. X' | Chegg.com
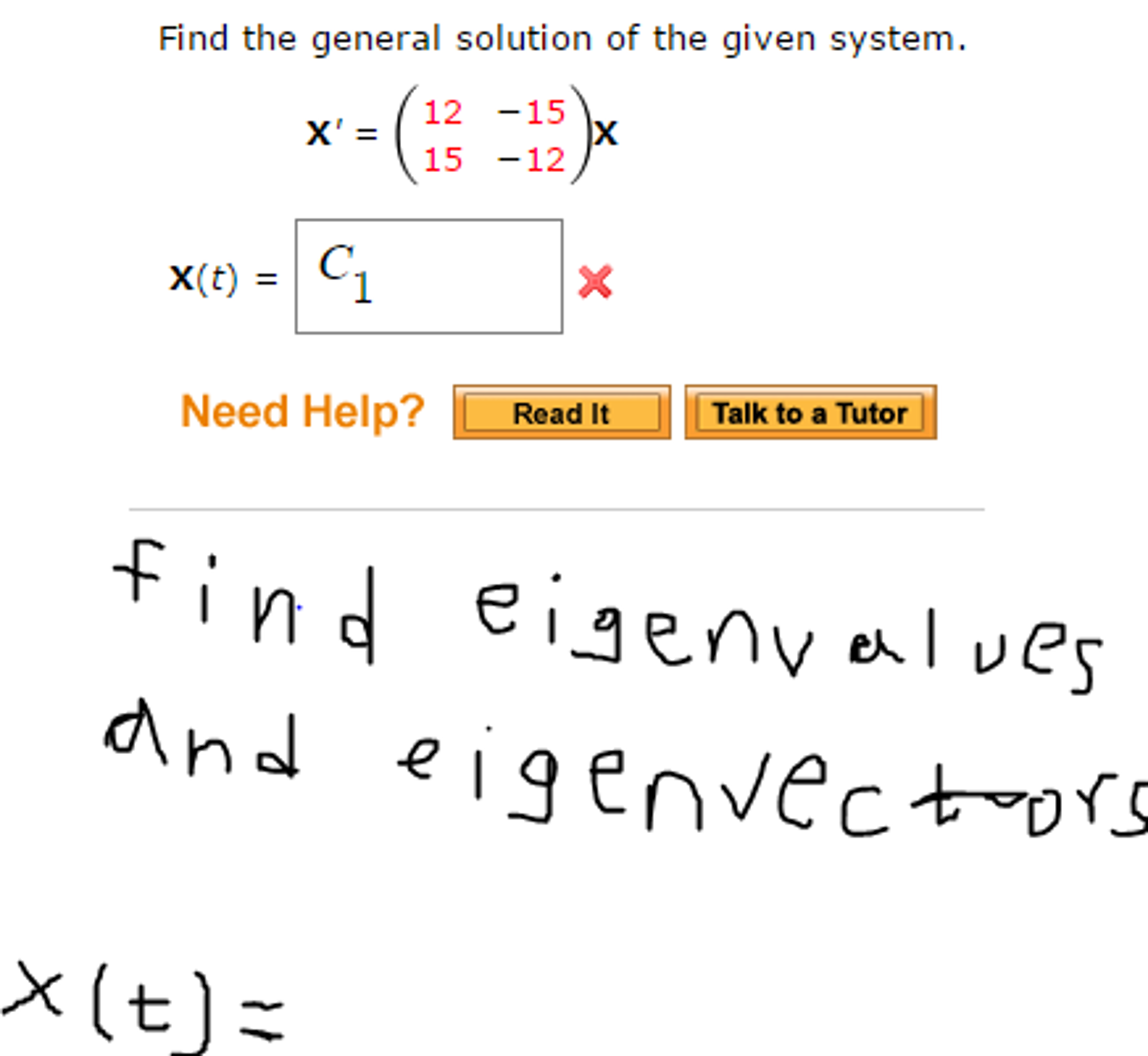 www.chegg.com
www.chegg.com given solution general system find transcribed text
Solved Find The General Solution Of The System Whose | Chegg.com
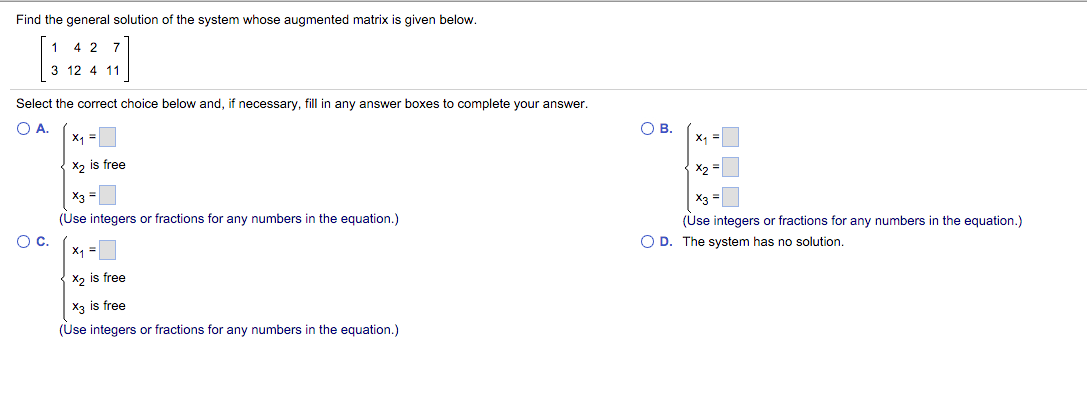 www.chegg.com
www.chegg.com whose solution general system find solved transcribed problem text been matrix augmented given
Solved Find The General Solution Of The Given System. X' = | Chegg.com
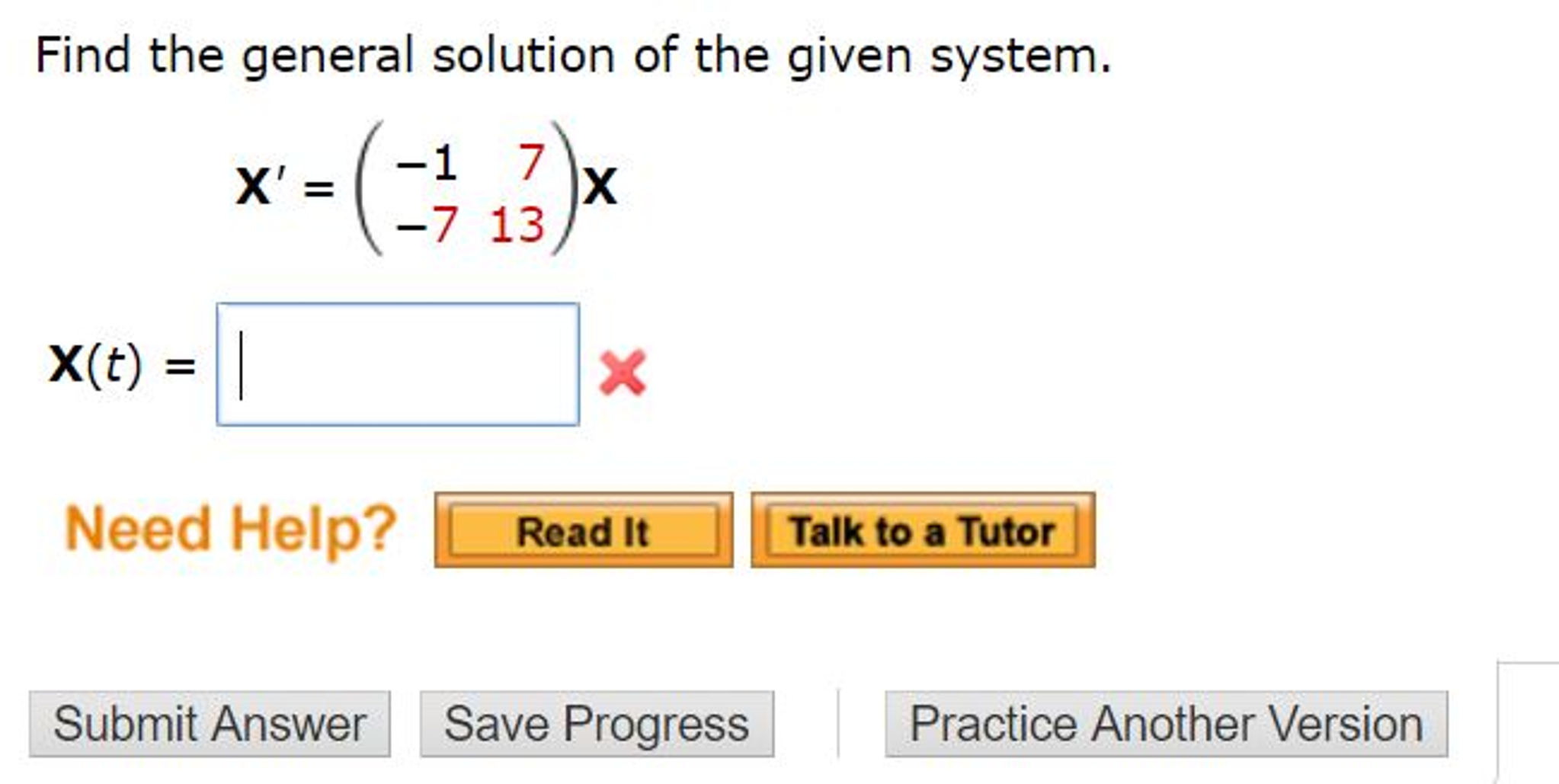 www.chegg.com
www.chegg.com given solution general system find transcribed text
Solved: Find The General Solution Of The Given System. X' | Chegg.com
 www.chegg.com
www.chegg.com given solution general system find
Solved Apply The Eigenvalue Method To Find A General | Chegg.com
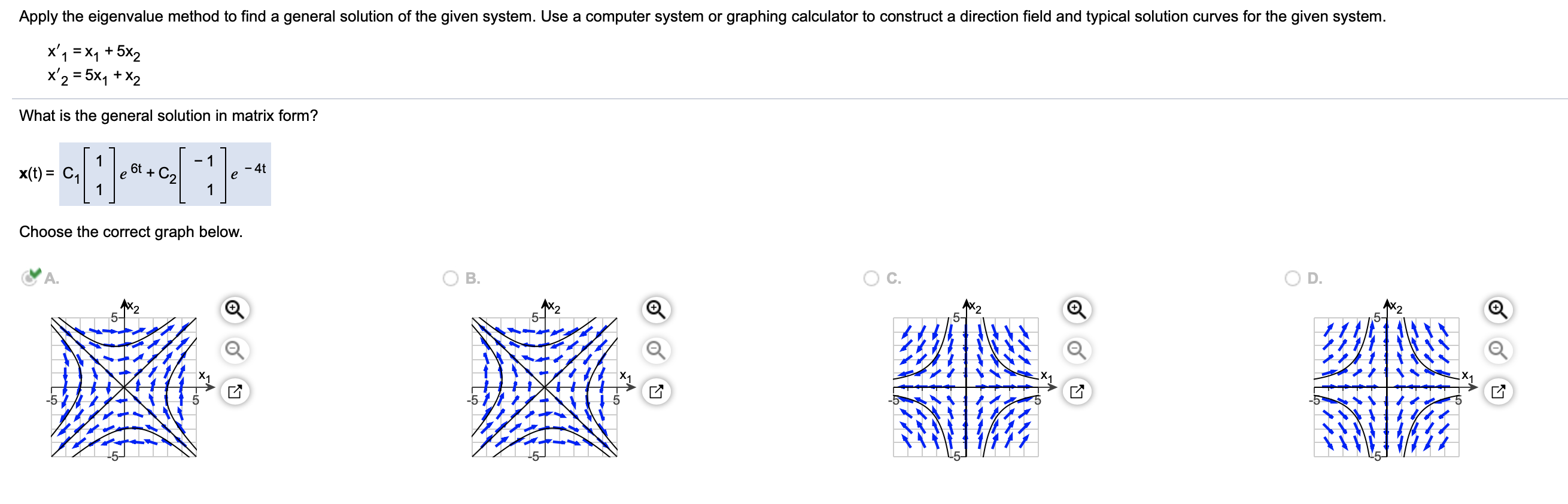 www.chegg.com
www.chegg.com eigenvalue graphing calculator
Solution general solved given system find transcribed problem text been. Given solution general system find transcribed text. Given solution general system find transcribed text

No comments:
Post a Comment