The concept of definite integrals is one of the fundamental topics of calculus, and it plays a crucial role in many different areas of mathematics and science. In this article, we will explore the definition of definite integrals and take a closer look at how they are used to solve real-world problems. At its most basic level, a definite integral can be thought of as a way to calculate the area under a curve. For example, suppose we have a function f(x) that represents the height of a curve at every point x. If we want to find the area under the curve between two points a and b, we can use the definite integral of f(x) from a to b to calculate that area. To calculate a definite integral, we first need to find the antiderivative of the function we are integrating. An antiderivative is simply a function that, when differentiated, gives us the original function. Once we have the antiderivative, we can evaluate it at the upper and lower limits of integration (in this case, a and b) and subtract the two values to find the area under the curve. One of the main benefits of using definite integrals is that they allow us to find exact values for areas under curves, volumes of objects with irregular shapes, and even the work done by a variable force over a given distance. This makes them incredibly useful in a wide range of fields, including physics, engineering, economics, and more. Now, let's take a closer look at the two images we have here. The first image displays the equation for a definite integral, which includes the upper and lower limits of integration and the function being integrated. Notice that the limits of integration are represented by a and b, which are shown at the top and bottom of the symbol. The second image shows an example of how to use definite integrals to find the area under a curve. In this case, we are finding the area under the function y = 2x between x = 0 and x = 2. To solve this problem, we first need to find the antiderivative of 2x, which is x^2. We then evaluate this antiderivative at the limits of integration (2^2 - 0^2) to find that the area under the curve is 4 square units. In conclusion, definite integrals are an incredibly powerful tool for calculating areas, volumes, and other important quantities in mathematics and science. By understanding their definition and how to use them properly, we can solve a wide range of problems and gain a deeper understanding of the world around us.
If you are looking for The Definition of The Definite Integral - YouTube you've came to the right place. We have 6 Pictures about The Definition of The Definite Integral - YouTube like The Definition of The Definite Integral - YouTube, The Definite Integral and also Integral - Wikipedia. Here you go:
The Definition Of The Definite Integral - YouTube
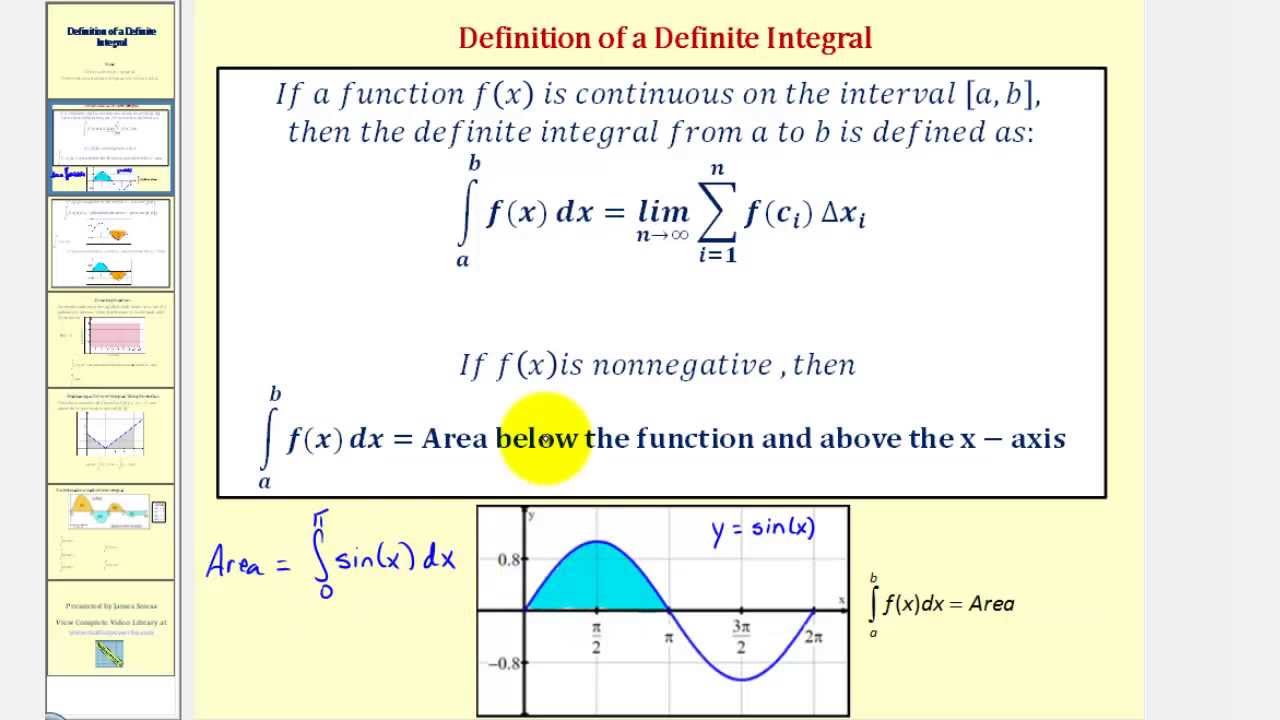www.youtube.com integral definition definite
Integral - Wikipedia
sco.wikipedia.org definite aurie
The Definite Integral
studylib.net integral definite definition closed doc
PPT - Introduction To Integrals PowerPoint Presentation, Free Download
www.slideserve.com definition definite integrals integral limit introduction limits lower
Definition Of Definite Integral - YouTube
www.youtube.com integral
Definite Integral Calculator | AtomsTalk
atomstalk.com definite calculus definida integrals integrales derivadas indefinite matematicas calculo atomstalk trucos matematicos matemáticas lecciones definidas
Definite aurie. Definition definite integrals integral limit introduction limits lower. The definite integral
No comments:
Post a Comment