differential calculus 101 Calculus differential formulas examples derivative dy

Differential calculus is an essential component of mathematics, specifically within the study of calculus. It involves the analysis of a mathematical function and its derivatives, which are used to calculate the rate of change of the function over time. With the help of differential calculus, we can easily find the slope of a curve, determine maximum or minimum values, and solve optimization problems. This post aims to provide you with two helpful visual aids that explain differential calculus's formulas and examples. The first image below shows you a comprehensive overview of the basic concepts in differential calculus, including key formulas and definitions. Each of these concepts is critical in studying calculus. The concepts are designed to help learners understand fundamental concepts to apply to more complex problems, such as the optimization of functions. The image explains the relationship between derivatives and tangent lines, as well as the concept of concavity or the curvature of a function's graph. As such, it is an excellent tool for those interested in grasping the fundamentals of differential calculus principles. 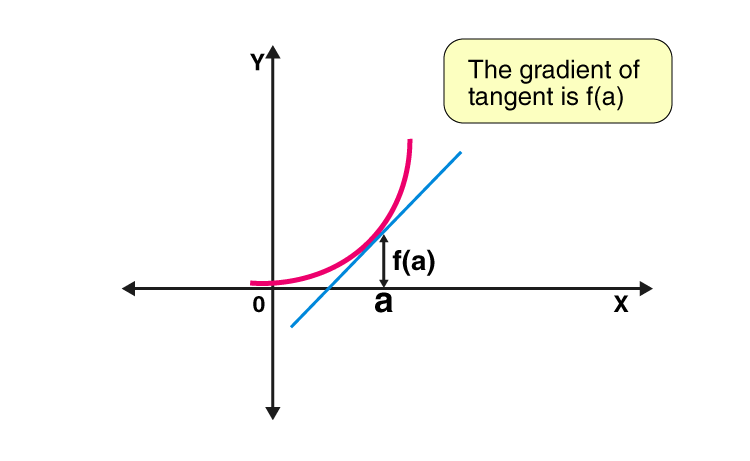For instance, the image shows you how to find the derivative of a function y=f(x) or dy/dx by applying differentiation rules. It also illustrates how to use the first derivative test to classify critical points as local maxima or minima. The first derivative test is essential in economics, engineering, and several other fields. Also, it helps with proving a function to be increasing, decreasing or constant on given intervals. In addition, the image demonstrates how to use the second derivative test to determine if a critical point is a maximum or minimum value. Another vital concept explained in the image is the chain rule, which is a technique for differentiating complex functions. Specifically, it is used when we have a function of a function. For instance, if we want to differentiate the f(g(x)), we apply the chain rule by first differentiating the outer function (f) and then the inner function (g). The image above gives you examples of how to apply the chain rule. The second visual aid below is an infographic that outlines the properties of derivatives. It shows the most important properties of derivatives in calculus, such as the product rule and quotient rule. Furthermore, it demonstrates how to use these rules to differentiate simple functions such as polynomials, trigonometric functions, and exponential functions.

Additional Properties of Derivatives Infographic

The properties of derivatives are fundamental in solving differential calculus problems. They enable learners to simplify calculations and develop effective methods to solve equations. For example, the chain rule and product rule are vital to solving problems with composite functions, whereas the quotient rule is used to find the derivative of a fraction. In summary, differential calculus can be challenging, but with the help of visual aids, learners can comprehend critical formulas and concepts more easily. The two visual aids presented in this post can help learners understand basic and advanced concepts of differential calculus, such as derivative rules and properties. Applying these techniques can help solve practical problems in real-life applications, such as physics or engineering.

If you are searching about Differential Calculus (Formulas and Examples) you've came to the right place. We have 6 Pictures about Differential Calculus (Formulas and Examples) like Differential Calculus Chapter 2, Differential Calculus (Formulas and Examples) and also Differential Calculus Photograph by Science Photo Library | Fine Art. Read more:

Differential Calculus (Formulas And Examples)

byjus.com

calculus differential formulas examples derivative dy

Differential Calculus | AdelaideX | University Of Adelaide

www.adelaide.edu.au

differential calculus adelaide applied relating concepts differentiation solve techniques problems discover real they

Differential Calculus Photograph By Science Photo Library | Fine Art

fineartamerica.com

calculus differential

Differential Calculus Chapter 2

math.byu.edu

differential calculus

Calculus I (Differential Calculus) | Math Fortress | Skillshare

www.skillshare.com

calculus differential math skillshare

Math Major 14 Differential Calculus Pw

www.slideshare.net

calculus differential

Differential calculus. Calculus differential. Math major 14 differential calculus pw