Calculus is a fundamental topic in mathematics that deals with concepts such as limits, derivatives, and integrals. In this post, we will focus on the basics of limits, which are pivotal in the study of calculus.
Introduction to Limits
The concept of limits is the foundation of calculus. A limit of a function is a value that the function approaches as the input variable gets closer to a particular value. The formal definition of a limit uses epsilon-delta notation, but we will not dive into that here.
Instead, we will look at limit notation that you may have seen before. For example, the limit of a function f(x) as x approaches a is written as:
limx→a f(x)
This notation represents the value that f(x) approaches as x gets arbitrarily close to a. Let’s see this in action with an example:
Limit Example
Consider the function f(x) = (x2 – 1) / (x – 1). If we evaluate f(x) at x = 1, we get the indeterminate form of 0/0. This means that we cannot simply substitute x = 1 into the function to find its value at x = 1.
However, we can use limit notation to find the value that f(x) approaches as x gets closer and closer to 1.
limx→1 (x2 – 1) / (x – 1)
We can factor the numerator to get:
limx→1 (x – 1)(x + 1) / (x – 1)
Notice that the (x – 1) terms in the numerator and denominator cancel out, leaving us with:
limx→1 (x + 1)
Now, we can simply substitute x = 1 to get:
limx→1 (x + 1) = 2
Therefore, the value of the limit of f(x) as x approaches 1 is 2.
Limit Laws
There are several laws that govern limits, which are crucial in finding limits of more complicated functions. Here is a brief summary of some of the key laws:
- Sum Law: This law states that the limit of the sum of two functions is equal to the sum of their limits. In other words:
limx→a [f(x) + g(x)] = limx→a f(x) + limx→a g(x)
- Product Law: This law states that the limit of the product of two functions is equal to the product of their limits. In other words:
limx→a [f(x) * g(x)] = limx→a f(x) * limx→a g(x)
- Quotient Law: This law states that the limit of the quotient of two functions is equal to the quotient of their limits. In other words:
limx→a [f(x) / g(x)] = [limx→a f(x)] / [limx→a g(x)]
There are many more laws governing limits, but these are the fundamental ones.
In summary, limits are a fundamental concept in calculus that are used to determine the value that a function approaches as the input variable gets closer to a particular value. Understanding limit notation and the laws governing limits is crucial to mastering this topic.
If you are looking for MakeTheBrainHappy: Limits in Calculus you've visit to the right place. We have 6 Pics about MakeTheBrainHappy: Limits in Calculus like MakeTheBrainHappy: Limits in Calculus, Calculus 1 - Introduction to Limits - YouTube and also Calculus Limits Worksheet With Answers - Worksheet List. Here it is:
MakeTheBrainHappy: Limits In Calculus
www.makethebrainhappy.com calculus limits ap pdf questions process collegeboard digitalservices secure sample source infinity
2-2 #58 | Math, Calculus, Limits | ShowMe
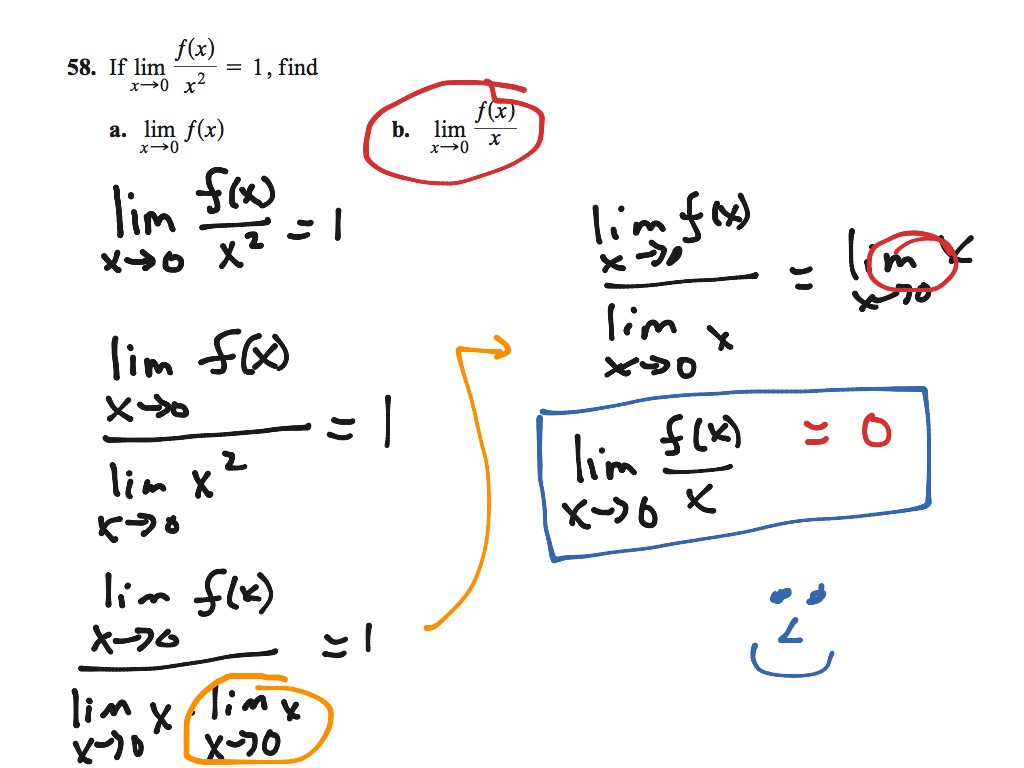www.showme.com calculus
Calculus 1 - Introduction To Limits - YouTube
www.youtube.com limits calculus introduction
AP Calculus AB Test Review Limits And Continuity Fall 2015 - YouTube
www.youtube.com calculus limits ap test ab continuity review
Limit Laws To Evaluate Understand Limits Ap Calculus AB BC Exam
www.pinterest.com limit limits calculus laws calc lim ap evaluate using bc ab understand math exam problems understanding lecture
Calculus Limits Worksheet With Answers - Worksheet List
nofisunthi.blogspot.com limits calculus worksheet finding khan academy answers strategy
Limits calculus worksheet finding khan academy answers strategy. Limit laws to evaluate understand limits ap calculus ab bc exam. Limits calculus introduction
No comments:
Post a Comment