Definite integrals are an important concept in mathematics, particularly in calculus. They refer to the process of calculating the area under a curve or the total amount of something over a given time period. Essentially, a definite integral is a sum of infinitely many tiny pieces, or infinitesimals, that make up the area or total amount.
Calculating Definite Integrals
There are a few methods for calculating definite integrals, including Riemann sums, the trapezoidal rule, and Simpson's rule. Generally, the preferred method is to use the fundamental theorem of calculus, which relates derivatives and integrals. To use this method, you need to first find the antiderivative, or indefinite integral, of the function you are working with. Then, you can use the antiderivative to calculate the definite integral by evaluating it at the upper and lower limits of integration.
For example, let's say we want to calculate the definite integral of f(x) = x^2 between x=0 and x=2. First, we need to find the antiderivative of f(x), which is F(x) = (1/3)x^3 + C, where C is the constant of integration. Next, we evaluate F(2) - F(0) to get the definite integral: (1/3)*(2^3) - (1/3)*(0^3) = 8/3.
Applications of Definite Integrals
Definite integrals have a wide range of applications in various fields, including physics, engineering, economics, and more. One common use of definite integrals is in calculating the work done by a force over a given distance. This can be represented graphically as the area under a force-distance curve.
Another application of definite integrals is in calculating the total mass, volume, or length of an object. For example, the mass of a thin wire can be calculated by integrating its linear density over its length. Similarly, the volume of a solid object can be found by integrating its cross-sectional area over its height.
Conclusion
Overall, definite integrals are a fundamental concept in calculus with a wide range of applications across various fields. While there are different methods for calculating definite integrals, the most common and efficient method is to use the fundamental theorem of calculus. By understanding the applications and properties of definite integrals, we can better appreciate their importance and the role they play in mathematical and scientific analysis.
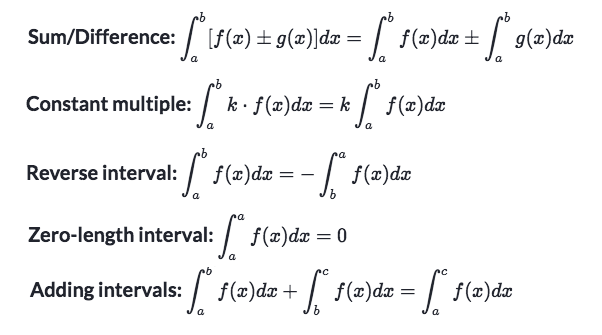
If you are looking for Solved V Use geometry to compute the following definite | Chegg.com you've came to the right place. We have 6 Pictures about Solved V Use geometry to compute the following definite | Chegg.com like Definite Integrals. DEFINITE means it’s defined, means both… | by, Definite Integrals - YouTube and also The Substitution Rule for Definite Integrals: Examples - YouTube. Read more:
Solved V Use Geometry To Compute The Following Definite | Chegg.com
www.chegg.com definite geometry compute following use integrals transcribed text
The Substitution Rule For Definite Integrals: Examples - YouTube
www.youtube.com substitution rule definite integrals examples
Solved Compute The Following Definite Integrals. (Be Sure To | Chegg.com
www.chegg.com solved compute integrals definite transcribed
Rápidamente Calcular Integrales Definidas Usando El Teorema Fundamental
maniqui.ru Definite Integrals. DEFINITE Means It’s Defined, Means Both… | By
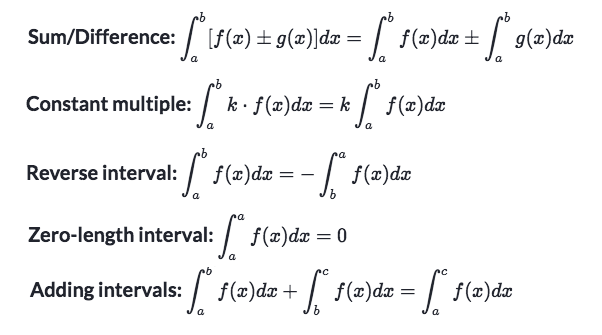medium.com definite integrals integral sum limit riemann properties basics calculus medium example
Definite Integrals - YouTube
www.youtube.com definite integrals
The substitution rule for definite integrals: examples. Solved compute integrals definite transcribed. Definite geometry compute following use integrals transcribed text
No comments:
Post a Comment