If you're someone who has trouble with calculus or math, specifically integral calculus, then there is good news! In this article, we will be discussing definite integrals and hopefully make it a little easier for you to grasp the concept.
The Basics of Definite Integrals
So, what exactly is a definite integral? Simply put, it is the calculation of the area under a curve between specified endpoints. Let's take a look at an example. If we have the function f(x) = x + x^2 and we want to calculate the definite integral from x = 0 to x = 2, we can use the following formula:
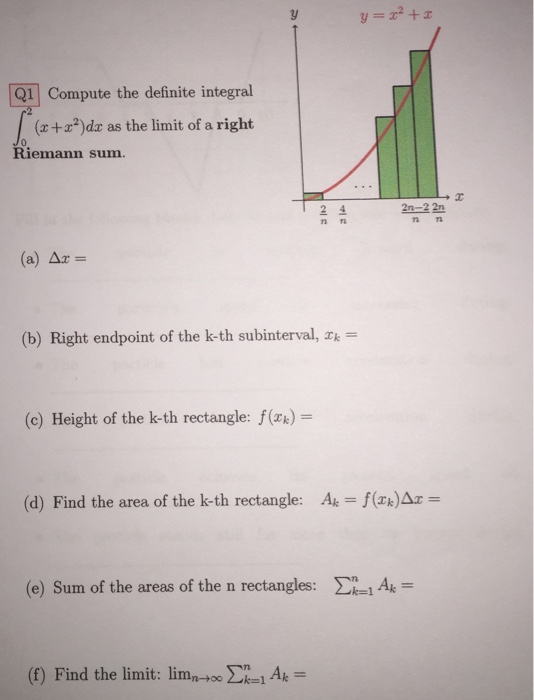
In this example, the area under the curve from x = 0 to x = 2 is equal to 4.67 (rounded to two decimal places).
Breaking It Down
Let's break down the formula to make it a little easier to understand.
- The integral sign ( ∫ ) signifies that we are performing an integration.
- The lower bound ( 0 ) signifies the starting point of the area under the curve.
- The upper bound ( 2 ) signifies the ending point of the area under the curve.
- The function ( x + x^2 ) is the function we are integrating.
- The dx signifies that we are integrating with respect to x.
Understanding definite integrals can be tricky, but the more you practice, the easier it will become. When looking at a definite integral, it's important to remember that you are finding the area under a curve between two specific endpoints.
Real World Applications
Definite integrals have many real world applications. For example, it can be used to calculate the displacement of an object over a certain period of time. If we have the velocity of an object over a specific time period, we can integrate the velocity function to find the displacement of the object over that time period.
Conclusion
Overall, definite integrals may seem intimidating at first, but with practice and patience, anyone can understand them. They have many real-world applications and can be used to solve a variety of problems. So, if you're struggling with integral calculus, don't be discouraged! Keep practicing and soon enough, you'll be a pro at definite integrals.
If you are looking for The Substitution Rule for Definite Integrals: Examples - YouTube you've came to the right place. We have 6 Images about The Substitution Rule for Definite Integrals: Examples - YouTube like Solved Compute the definite integral integral^2 _0 (x +x^2) | Chegg.com, Definite Integrals - YouTube and also The Substitution Rule for Definite Integrals: Examples - YouTube. Read more:
The Substitution Rule For Definite Integrals: Examples - YouTube
www.youtube.com substitution rule definite integrals examples
Solved Compute The Definite Integral Integral^2 _0 (x +x^2) | Chegg.com
www.chegg.com compute definite
Ex: Definite Integrals As Area Given A Graph (Function) - YouTube
www.youtube.com integrals definite
Definite Integrals - YouTube
www.youtube.com definite integrals
Definite Integrals. DEFINITE Means It’s Defined, Means Both… | By
medium.com definite integrals calculus
Solved Compute The Definite Integral As The Limit Of Riemann | Chegg.com
www.chegg.com limit integral riemann compute definite sums dx transcribed text 4x
Solved compute the definite integral as the limit of riemann. Substitution rule definite integrals examples. Definite integrals calculus
No comments:
Post a Comment